- 3.1 引言
- 小数和其他实数如何表示
- 当一个操作生成了一个无法表示的大数时如何处理
- 怎么用硬件真正地做乘法和除法
- 3.2 加法和减法
- 溢出
- 硬件有一定规模,当运算结果超过这个限制时,就会发生溢出
- 正数+正数=负数,负数+负数=正数 就是发生了溢出
- 算术逻辑单元(ALU):用于执行加法、减法,通常也包括逻辑与、逻辑或等逻辑操作的硬件
- 异常:也叫中断,一种打断正常程序执行过程的事件,用于溢出检测
- 中断:来自处理器外部的异常
- 3.3 乘法
- 1)当乘数位为1时,只需要将被乘数(1X被乘数)复制到合适的位置
- 2)当乘数位为0时,将0放置到合适的位置
- 3.3.1 顺序的乘法和硬件

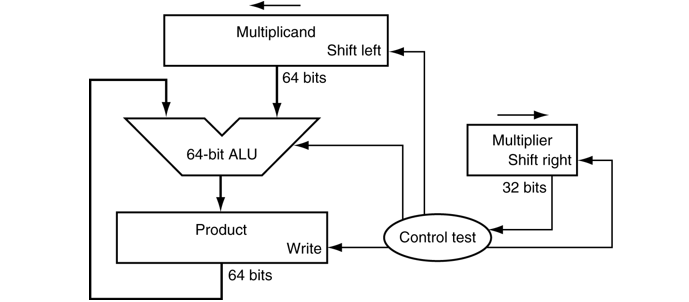
- 第一版乘法器
- 被乘数寄存器、ALU和积寄存器都是64位长,而乘数寄存器是32位长
- 32位的被乘数开始被放在被乘数寄存器的右半部分。然后每次左移一位。
- 乘数寄存器则向相反方向移动。
- 算法开始时,积被初始化为0。
- 控制逻辑决定何时对被乘数和乘数寄存器进行移位,以及何时将新值写入寄存器

- 改进版
- 并行化来加速执行
- 当乘数位为1时,将乘数和被乘数进行移位,同时将被乘数和积相加。
- 除了积寄存器为64位,其他寄存器为32位
- 3.3.2 有符号乘法
- 3.3.3 更快速的乘法
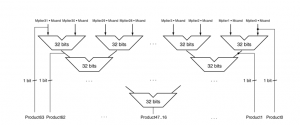
- 为乘数的每一位提供一个32位的加法器:一个用来输入被乘数和一乘数位相与的结果,另一个上一个加法器的输出
- 事实上,通过使用进位保留加法器,乘法的计算速度可以快于五次加法,而且易于应用流水线设计执行,这样的结果可以同步支持多个乘法运算
- 3.3.4 MIPS中的乘法
- MIPS提供了一堆单独的32位寄存器来容纳64位的积,称为Hi和Lo
- MIPS提供了两条指令:mult与无符号乘法multu
- 为了取得32位的整数积,程序员需要使用mflo指令
- MIPS汇编器为乘法生成了一条伪指令,它使用了三个通过寄存器,用mflo和mfhi指令将积送入指定的寄存器
- 3.3.5 小结
- 乘法硬件只是简单地移位和加法
- 通过使用更多硬件的方法,可以做到并行做加法操作,从而提高运算速度
- 3.4 除法
- 3.5 浮点运算
- 科学计数法与规格化
- 浮点数:二进制小数点不固定的表达数的记数法
- 采用规格化形式的标准科学计算法有三个优势:简化了浮点数的数据交换;简化了浮点算术算法;提高了用一个字存储的数的精度。因为无用的前导0可能占用的位被二进制小数点右边的有效位替代了。
- 3.5.1 浮点表示
- 浮点表示的设计者必须在尾数位宽和指数位宽之间找出折中的办法
- 增加小数部分会提高数的表示精度,增加指数部分会增加数的表示范围
- MIPS中,s为浮点数的符号(1表示负数),指数域为8位宽(包括指数的符号位),尾数域为23位宽
- 这种表示称为符号和数值
- (-1)^s * F * 2 ^ E
- F为小数域的值,E为指数域的值
- 范围2.0*1e-38 ~ 2.0*1e38
- 溢出(上溢):正的指数太大而导致指数域放不下的情况
- 下溢:负的指数太大而导致指数域放不下的情况
- 双精度:浮点数由两个32位的字表示
- 单精度:浮点数由一个32位的字表示
- IEEE 754
- 3.5.2 浮点加法
- 3.5.3 浮点乘法
- 3.5.4 MIPS中的浮点指令
- 3.5.5 算术精确性
- 3.6 并行性和计算机算术:子字并行
- 3.7 实例:X86中流处理SIMD扩展和高级向量扩展
- 3.8 加速:子字并行和矩阵乘法
- 3.9 谬误与陷阱
- 谬误:正如正数乘法中左移指令可以代替与2的幂次方数相乘一样,右移指令也可以代替与2的幂次方数相处
- 陷阱:浮点加法是不能使用结合律的
- 谬误:并行策略不但适用于整型数据类型,同样也适用于浮点数据类型
- 陷阱:MIPS指令addiu(无符号立即加)会对16位立即数域进行符号拓展
- 谬误:只有理论数学家才会关心浮点精度
- 3.10 总结
- 。。。
- 一些指令被编译器接受但不属于MIPS-32的指令,我们称为伪MIPS指令集