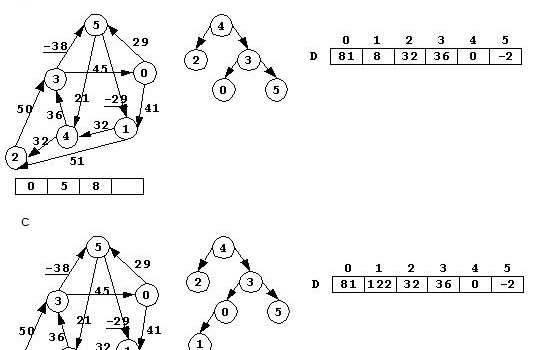
Bellman – ford算法是求含负权图的单源最短路径的一种算法,效率较低,代码难度较小。其原理为连续进行松弛,在每次松弛时把每条边都更新一下,若在n-1次松弛后还能更新,则说明图中有负环,因此无法得出结果,否则就完成。
复杂度:O(NM)
Dijkstra算法无法判断含负权边的图的最短路。如果遇到负权,在没有负权回路(回路的权值和为负,即便有负权的边)存在时,也可以采用Bellman – Ford算法正确求出最短路径。
Bellman-Ford算法能在更普遍的情况下(存在负权边)解决单源点最短路径问题。对于给定的带权(有向或无向)图 G=(V,E), 其源点为s,加权函数 w是 边集 E 的映射。对图G运行Bellman – Ford算法的结果是一个布尔值,表明图中是否存在着一个从源点s可达的负权回路。若不存在这样的回路,算法将给出从源点s到 图G的任意顶点v的最短路径d[v]。
适用条件
1.单源最短路径(从源点s到其它所有顶点v);
2.有向图&无向图(无向图可以看作(u,v),(v,u)同属于边集E的有向图);
3.边权可正可负(如有负权回路输出错误提示);
4.差分约束系统;
算法描述
1,.初始化:将除源点外的所有顶点的最短距离估计值 d[v] ——>+∞, d[s]——>0;
2.迭代求解:反复对边集E中的每条边进行松弛操作,使得顶点集V中的每个顶点v的最短距离估计值逐步逼近其最短距离;(运行|v|-1次)
3.检验负权回路:判断边集E中的每一条边的两个端点是否收敛。如果存在未收敛的顶点,则算法返回false,表明问题无解;否则算法返回true,并且从源点可达的顶点v的最短距离保存在 d[v]中。
描述性证明
首先指出,图的任意一条最短路径既不能包含负权回路,也不会包含正权回路,因此它最多包含|v|-1条边。
其次,从源点s可达的所有顶点如果 存在最短路径,则这些最短路径构成一个以s为根的最短路径树。Bellman-Ford算法的迭代松弛操作,实际上就是按每个点实际的最短路径[虽然我们还不知道,但它一定存在]的层次,逐层生成这棵最短路径树的过程。
注意,每一次遍历,都可以从前一次遍历的基础上,找到此次遍历的部分点的单源最短路径。如:这是第i次遍历,那么,通过数学归纳法,若前面单源最短路径层次为1~(i-1)的点全部已经得到,而单源最短路径层次为i的点,必定可由单源最短路径层次为i-1的点集得到,从而在下一次遍历中充当前一次的点集,如此往复迭代,[v]-1次后,若无负权回路,则我们已经达到了所需的目的–得到每个点的单源最短路径。[注意:这棵树的每一次更新,可以将其中的某一个子树接到另一个点下]
反之,可证,若存在负权回路,第[v]次遍历一定存在更新,因为负权回路的环中,必定存在一个“断点”,可用数学手段证明。
最后,我们在第[v]次更新中若没有新的松弛,则输出结果,若依然存在松弛,则输出‘CAN’T’表示无解。同时,我们还可以通过“断点”找到负权回路。
伪代码:
bool Bellman-Ford(G,w,s) //图G ,边集 函数 w ,s为源点
1 for each vertex v ∈ V(G) //初始化 1阶段
2 d[v] ←+∞;
3 d[s] ←0; //1阶段结束
4 for(int i=1;i<|v|;i++) //2阶段开始,双重循环。
5 for each edge(u,v) ∈E(G) //边集数组要用到,穷举每条边。
6 if(d[v]> d[u]+ w(u,v))//松弛判断
7 d[v]=d[u]+w(u,v); //松弛操作2阶段结束
8 for each edge(u,v) ∈E(G)
9 if(d[v]> d[u]+ w(u,v))
10 return false;
11 return true;
时间复杂度
算法时间复杂度O(VE)。因为算法简单,适用范围又广,虽然复杂度稍高,仍不失为一个很实用的算法。
初始状态:
0 inf inf … inf inf
简单代码:
for(int i = i ; i<= n; i++) dis[i] = inf;
dis[1] = 0;
for(int k = 1; k <= n-1; k++){//次数为顶点数减一
for(int i = 1; i <= m ; i++){//边数
if(dis[u[i]] != inf&&dis[v[i]] > dis[u[i]] +w[i]){//这里有个一开始设置为无限的值,应先进行判断再进行比较
dis[v[i]] = dis[u[i]] + w[i];
}
}
}
flag = 0;
//结束后再进行一轮以检测是否有负权回路
for(int i = 1; i <=m ; i++)
if(dis[v[i]] > dis[u[i]] + w[i]) flag = 1;
if(flag == 1) printf("此图含有负权回路");
更为一般的模板:
/*
* 单源最短路bellman_ford算法,复杂度O(VE)
* 可以处理负边权图。
* 可以判断是否存在负环回路。返回true,当且仅当图中不包含从源点可达的负权回路
* vector<Edge>E;先E.clear()初始化,然后加入所有边
* 点的编号从1开始(从0开始简单修改就可以了)
*/
const int INF=0x3f3f3f3f;
const int MAXN=550;
int dist[MAXN];
struct Edge
{
int u,v;
int cost;
Edge(int _u=0,int _v=0,int _cost=0):u(_u),v(_v),cost(_cost){}
};
vector<Edge>E;
bool bellman_ford(int start,int n)//点的编号从1开始
{
for(int i=1;i<=n;i++)dist[i]=INF;
dist[start]=0;
for(int i=1;i<n;i++)//最多做n-1次
{
bool flag=false;
for(int j=0;j<E.size();j++)
{
int u=E[j].u;
int v=E[j].v;
int cost=E[j].cost;
if(dist[v]>dist[u]+cost)
{
dist[v]=dist[u]+cost;
flag=true;
}
}
if(!flag)
return true;//没有负环回路
}
for(int j=0;j<E.size();j++)
if(dist[E[j].v]>dist[E[j].u]+E[j].cost)
return false;//有负环回路
return true;//没有负环回路
}
模板2:FIFO队列优化
Spfa是Bellman-Ford算法利用队列的优化,Bellman-Ford算法存在大量的无效松弛,spfa对它进行改进,对于每个点只松弛与这个点相关的边。
该优化和Dijkstra算法很相似,一方面,优先队列替换成了普通的FIFO队列,另一方面,一个结点可以多次进入队列。
/*
* 单源最短路SPFA
* 时间复杂度 0(kE)
* 这个是队列实现,有时候改成栈实现会更加快,很容易修改
* 这个复杂度是不定的
*/
const int MAXN=1010;
const int INF=0x3f3f3f3f;
struct Edge
{
int v;
int cost;
Edge(int _v=0,int _cost=0):v(_v),cost(_cost){}
};
vector<Edge>E[MAXN];
void addedge(int u,int v,int w)
{
E[u].push_back(Edge(v,w));
}
bool vis[MAXN];//在队列标志
int cnt[MAXN];//每个点的入队列次数
int dist[MAXN];
bool SPFA(int start,int n)
{
memset(vis,false,sizeof(vis));
for(int i=1;i<=n;i++)
dist[i]=INF;
vis[start]=true;
dist[start]=0;
queue<int>que;
while(!que.empty())
que.pop();
que.push(start);
memset(cnt,0,sizeof(cnt));
cnt[start]=1;
while(!que.empty())
{
int u=que.front();
que.pop();
vis[u]=false;
for(int i=0;i<E[u].size();i++)
{
int v=E[u][i].v;
if(dist[v]>dist[u]+E[u][i].cost)
{
dist[v]=dist[u]+E[u][i].cost;
if(!vis[v])
{
vis[v]=true;
que.push(v);
if(++cnt[v]>n) //cnt[i]为入队列次数,用来判定是否存在负环回路
return false;
}
}
}
}
return true;
}