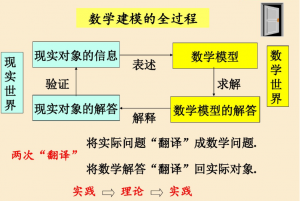
实际问题转化为数学问题,数学问题的求解,数学解答回归实际问题,这整个过程称为数学建模,即为实际问题建立数学模型。
1.1 从现实对象到数学建模
常见的有实物模型(玩具、照片、飞机)、物理模型(水箱中的舰艇、风洞中的飞机)、符号模型(地图、电路图、分子结构图)
模型是为了一定目的,对客观事物的一部分进行减缩、抽象、提炼出来的原型的替代物,集中反映了原型中人们需要的那一部分特征。
举个简单的例子,初中物理或者是小学数学中的“航行问题”
航行问题建立数学模型的基本步骤:
- 做出简化假设(船速、水速为常数)
- 用符号表示有关量(x,y)
- 用物理定律列出数学式子
- 求解得到数学解答
- 回答原问题
如此看来,我们并非首次接触数学建模,只是我们接触的模型都较为简单,或者我们常常在思考实际问题时,都会将数学建模的步骤简化,只求个大概(譬如我经常思考问题时用直觉解决)
数学模型:
对于一个现实对象,为了一个特定目的,根据其内在规律,作出必要的简化假设(这点很重要,比如讨论车的运动,可能实际上并不是简单的加减速,但在数学建模时,应该选择简单可靠的假设求解),运用适当的数学工具,得到一个数学表述。
数学建模:
建立数学模型的全过程(表述、求解、解释、检验等)
1.2 数学建模的重要意义
跳过,我不想听
1.3 简单建模示例之——包饺子中的数学
question:通常,1kg面包1kg馅,但是今天,我多买了馅,我有强迫症,要刚好用完皮和馅,我该多包几个(包小一些),还是少包几个(包大一些)?
分析:我妈肯定会把多余的馅用来煎蛋,问题解决。
实际上,我们需要比较的是馅和面增加的数量关系。
同船速问题,我们先做出
假设:
皮一样厚,形状一样
建模:S=ns(1) 面积公式中的k1与体积公式中的k2分别都相同
解释:
 (nv为n个小饺子的体积也就是馅的量(假设饺子质量馅分布均匀,质量与体积正比))
(nv为n个小饺子的体积也就是馅的量(假设饺子质量馅分布均匀,质量与体积正比))
定性分析:V比nv大——同样多的面,大饺子包的馅多
定量结果:V是nv的sqrt(n)倍
应用:
面皮同样多,100个饺子包1kg馅,50个包多少馅?
V=sqrt(n1)(n1v1)=sqrt(n2)(n2v2),解得n2v2为1.414kg
讨论:该建模过程由于假设了厚度相同,所以约去了半径的影响,但是如果厚度与半径成正比呢?那是否意味着讨论时需要加入常量R与r,导致无法解决问题?并不是。M正比于SR,最后V=nv,也就是说,当厚度与半径成正比时,在假设条件下,大饺子和小饺子的面与馅的消耗成正比,多出来的馅,只能让我妈煎蛋了。可是我有强迫症,可以尝试对数、幂次、指数,然后可以尝试着假设使得水饺煮不漏的最小厚度与馅重量的关系(感觉这就复杂了,不同面的不同受力,面皮溶解于水的程度,等学有所成,再回头看这题)。
1.4 建模示例之路障间距的设计
没啥好说的,只是在拟合过程中,可以使用线性的最小二乘法,代码如下:
X=[0 10 20 30 40]; Y=[0 1.6 3.0 4.2 5.0]; n=5; %一共5个变量 x2=sum(X.^2); % 求Σ(xi^2) x1=sum(X); % 求Σ(xi) x1y1=sum(X.*Y); % 求Σ(xi*yi) y1=sum(Y); % 求Σ(yi) a=(n*x1y1-x1*y1)/(n*x2-x1*x1) %解出直线斜率b=(y1-a*x1)/n b=(y1-a*x1)/n; %解出直线截距 %作图 % 先把原始数据点用蓝色十字描出来 figure plot(X,Y,'+'); hold on % 用红色绘制拟合出的直线 px=linspace(0,60,45);%这里直线区间根据自己实际需求改写 py=a*px+b; plot(px,py,'r')
其实matlab有内置函数线性最小二乘法
x=[0 10 20 30 40]; y=[0 1.6 3.0 4.2 5.0]; p=polyfit(x,y,1) y2=polyval(p,x); plot(x,y,'r*',x,y2,'b')
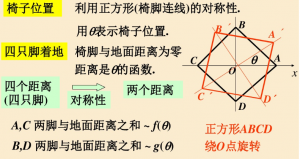
1.5 建模示例之椅稳否
问题:不平的地面上放着一张椅子,然而从实际生活中我们可以感受到,椅子常常只有三只脚着地,椅子能在不平的地面上放稳吗?
假设:
- 没有长短腿,四角正方形
- 地面为连续曲面
- 地面相对平坦,至少三只脚着地
- 将椅子脚最低端看作一个点
模型建立:
- 地面为连续曲面-》f(theta),g(theta)均为连续函数 (这点十分重要,因为要运用初等函数的性质)
- 椅子在任意位置至少三只脚着地-》f*g=0;
- 椅子旋转九十度,对角线互换-》g(0)=0,f(0)>0,f(pi/2)=0,g(pi/2)>0
所以可以将命题改为:
已知:f(theta),g(theta)连续,对任意theta,f*g=0,且g(0)=f(pi/2)=0,f(0)>0,g(pi/2)>0.
证明:存在theta0,使得f(theta0)=g(theta0)=0.
(感觉这里用到了计算机的思维,只关心0与非0)
模型求解:
- 令h(theta)=f(theta)-g(theta),则h(0)>0,h(pi/2)<0.
- h连续(初等函数连续性)
- 零点存在定理
- f(theta0)*g(theta0)=0,f(theta)-g(theta)=0 —》 f(theta0)=g(theta0)=0;
在该模型下,一定能找到,但是,如果旋转轴不是中点呢?如果椅子是非正方形的矩形呢?如果地面是分段函数呢?Ma着,慢慢解决。
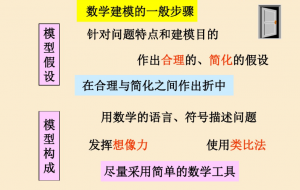
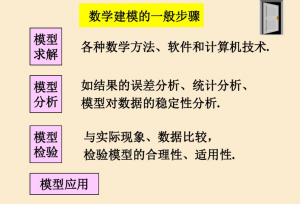
1.6 数学建模的基本方法和步骤
数学建模的基本方法:
机理分析:对客观事物特性的认识,内部机理的数量规律 白箱
测试分析:对量测数据的统计分析,与数据拟合最好的模型 黑箱
二者结合:机理分析建立模型结构,测试分析确定模型参数 灰箱
机理分析主要通过案例研究学习,建模主要指机理分析(所以一个月能不能看足够多的样例呢)
1.7 数学模型的特点和分类
特点:
逼真性和可行性 、非预制性、渐近性、条理性、强健性、技艺性、可转移性、局限性。
分类:
应用领域:人口、交通、经济、生态、……
数学方法:初等数学、微分方程、规划、统计、……
表现特性:确定和随机 静态和动态 离散和连续 线性和非线性
建模目的:描述、优化、预报、决策、……
了解程度:白箱 灰箱 黑箱
1.8 如何学习数学建模
- 培养意识和能力
- 想象力 洞察力 判断力 创新意识 数学知识 决心与能力
- 学习、分析、改进、推广
- 实际题目、参加竞赛