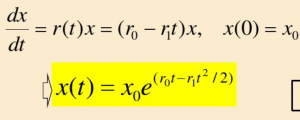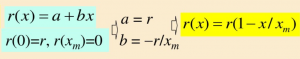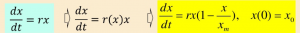撰写
- 微分方程：含自变量、未知函数及其导数的方程。
- 描述时间连续变化物体或过程的动态变化规律。
- 采用机理分析或类比法建立微分方程。
物理领域：工程技术、科学研究（牛顿定理 电路原理）
例. 火箭发射——由燃料燃烧推力发射的火箭加速度、速度、高度的微分方程。
非物理领域：人口、经济、生态等（特定的内在规律）
例.人口预测——含人口数量及增长率的微分方程。
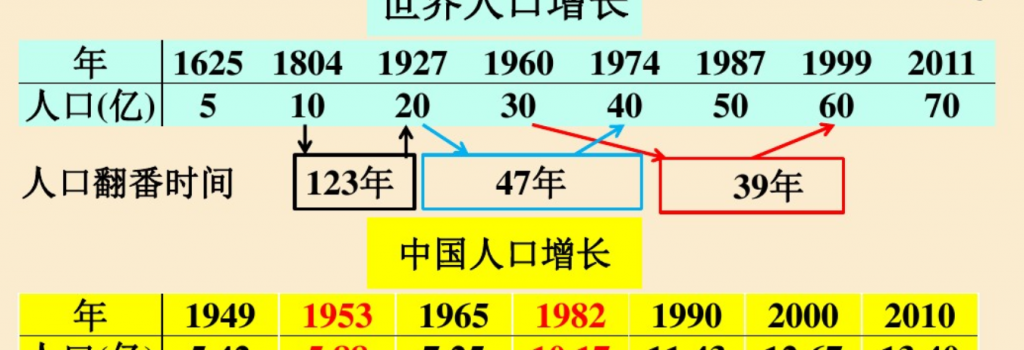
人口增长预测：
- 20世纪的一段时间内人口增长素的过快
- 年净增人口由最多的2000多万降到2011年的600多万
- 老龄化提速，性别比失调等凸显，开始调整人口政策
- 两个基本的人口模型
- 用美国人口估计参数
- 模型检验和增长预测
指数增长模型：
1.一个常用的人口预测模型
已知今年人口为x0，年增长率r，k年后的人口为
（基本前提：增长率r在k年内保持不变）
- 已知增长率预测未来人口
- 根据人口估计增长率
r=(ln2)/k 为啥-》 （求解
即可证明）
2.人口指数增长模型的建立
假设：
- t时刻人口数量为连续、可微函数x(t)
- 单位时间人口的增长率为常熟r
- 初始时刻(t=0)的人口为x0
模型：单位时间内x(t)的增量为rx(t)
由一阶线性微分方程中的可分解形式解得
3.指数增长模型的参数估计（数据拟合）
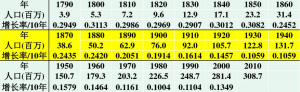
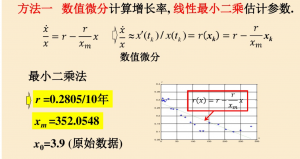
方法一 直接用人口数据和线性最小二乘法
两边取对数
最小二乘法matlab计算 r=0.2743/10年，x0=4.1884
方法二 对人口数据作数值微分估计增长率
- 取各点附近导数值
- 求各点增长率
- 取平均值 （应该是n-1个区域而非n+1个）
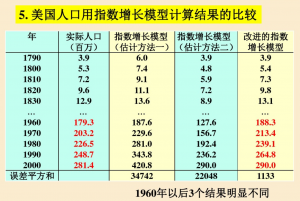
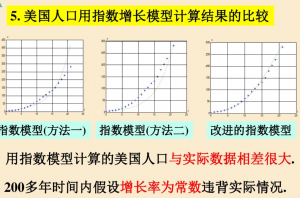
但是，用假设的模型计算与实际数据差距很大，这是由于我们假设了增长率r为常数的缘故。
4.改进的指数增长模型
假设r(t)=r0-r1t(可以用线性最小二乘法拟合)
线性最小二乘法拟合 r0=0.3252, r1=0.0114,x0=3.9（原始数据）
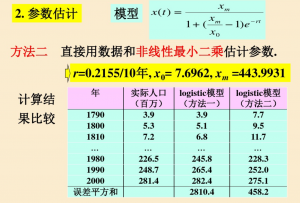
5.比较
6.指数增长模型的应用及局限性
- 与19世纪以前欧洲一些地区人口统计数据吻合
- 使用于19世纪后迁往加拿大的欧洲移民后代
- 不符合19世纪后多数地区人口增长规律
- 可以用于短期而不能用于长期的人口预测
- 未考虑科技、医学的重大进步的影响（比如第一、二次工业革命）
- 改进的指数模型计算结果有所改善，但它仍然未反映增长率下降的机理，函数形式也不易确定，不便于应用
所以，需分析人口增长率下降的机理，修改假设建立新模型。
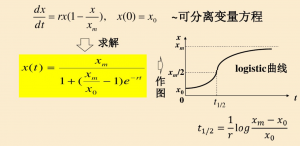
logistic模型
1.模型建立
- 人口增长到一定数量后增长率下降的原因——资源、环境等因素对人口增长的阻滞作用，且组织作用随着人口增大而变大。（r是x的减函数）
- 简单、便于应用的线性函数r(x)=a+bx
固有增长率r：理论上x=0时的增长率 r(0)=r
人口容量xm:资源和环境对人口的最大容量 r(xm)=0
2.参数估计
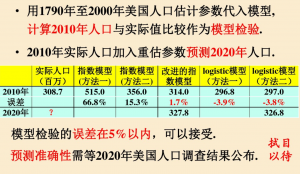
3.模型检验和人口预测
小结与评注：
- 模型假设是建模的关键之一，“增长率随人口增加而线性减少”是logistic模型的合理、简化假设
- 参数估计是建模的重要步骤，最小二乘法是参数估计的基本方法
- 模型检验对建模是不可缺少的，用作检验的数据不应用于建模过程的参数估计