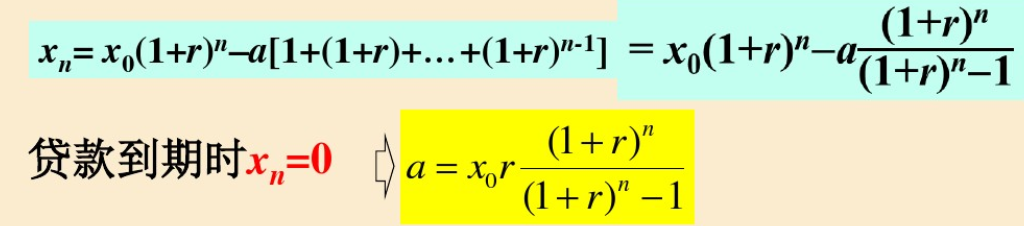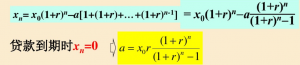6.1 贷款买房

• 差分方程：若干离散点上位置变量数值的方程
• 描述离散时间段上客观对象的动态变化过程
• 现实世界中随时间连续变化的动态过程的近似
• 差分方程与代数方程都是离散模型的数学表述，二者有着类似的向量-矩阵表达形式，求解过程也存在相互联系

贷款买房-最简单的差分方程模型

问题：买多大的房子，一共贷多少钱，每月还款几何？

单利和复利：

两种计算利息的基本方式

• 单利：1W存5年定期，年利率4.75%，到期后本息12375元（单利本息：1+nr）
• 复利：1w存1年定期，年利率3.00%，到期后不取自动转存，五年后本息：11593元（复利本息：（1+r）^n>1+nr）

按单利计算的业务——零存整取

• 零存整取：每月固定存额，约定存款期限，到期一次支取本息的定期储蓄
• 方式：5元起存，多存不限，存期1，3，5年
• 例：每月存3000元，存期5年，年利率5%，累计存入18000元，到期本息总额196012.50元

a：每月存入金额      r：月利率      n：存期（月） xk：存入k个月之后的本息     

得到：

等额本息贷款和等额本金贷款：

房贷计算器的选项：

• 贷款类别：商业贷款、公积金、组合型   （ 年利率不同）
• 计算方法：根据贷款总额或面积、单价计算
• 按揭年数：可选1至30年 （选择20年）
• 还款方式：等额本息还款或等额本金还款
  • 等额本息还款：每月归还本息数额相同
  • 等额本金还款：每月归还本金相同，加上所欠本金的利息（所欠本金逐月减少-》每月还款金额递减）
• 例：选择等额本息还款，总额100w，期限20年，年利率6.55%—-》还款总额1796447.27元，月均还款7485.2元

等额本息还款模型：

x0：贷款总额r：月利率 n：贷款期限 xk：第k月还款后尚欠金额 a：每月还款金额(本月欠额=上月欠额的本息-还款金额)

，k=n递推至k=1

等额本金还款模型：

 

并不一定，要保证其余条件不变以及选择还款方式相同。