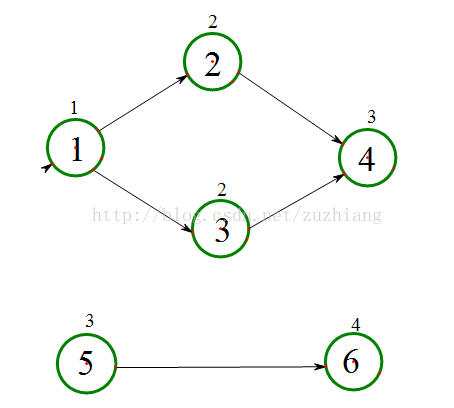
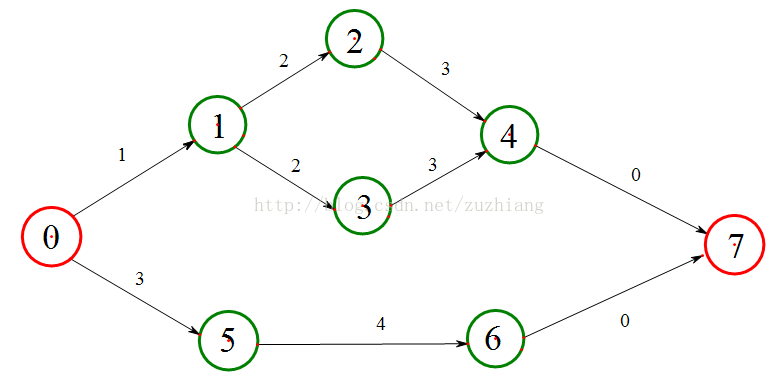
#include<stdio.h>
#include<string.h>
#include<iostream>
#include<queue>
#define inf 0x3f3f3f3f
using namespace std;
typedef long long LL;
int n,m;
int tol,cnt,head[100010]; //链式前向星
//w记录点权,chu记录点的出度,ru记录点的入度,que记录拓扑序列
int w[100010],chu[100010],ru[100010],que[100010];
//dis记录点到源点的最大距离
LL dis[100010];
queue<int> Q;
struct node
{ //链式前向星
int w,to,next; //分别为边权、终点和以u为起点的下一条边在的位置
} edge[2000010];
void init()
{ //初始化函数
tol=0;
memset(head,-1,sizeof(head));
memset(chu,0,sizeof(chu));
memset(ru,0,sizeof(ru));
}
void add(int u,int v,int w)
{ //加边函数
edge[tol].w=w;
edge[tol].to=v;
edge[tol].next=head[u];
head[u]=tol++;
}
void tuopu()
{ //获得拓扑排序
int i,j,top;
cnt=0;
dis[0]=0;
Q.push(0); //0点入队
for(i=1;i<=n+1;i++) dis[i]=-inf; //初始化最长距离为最小值
while(!Q.empty())
{ //只有减边的点才有可能入度为0
top=Q.front();
Q.pop();
que[cnt++]=top; //保存拓扑序列
ru[top]--; //当前节点入度-1
for(j=head[top];j!=-1;j=edge[j].next)
{ //遍历与top相连的节点
ru[edge[j].to]--; //入度-1
if(ru[edge[j].to]==0) Q.push(edge[j].to); //如果入度为0则入队
}
}
}
void solve()
{
int i,j,v;
for(i=0;i<cnt;i++) //依照拓扑序列处理
for(j=head[que[i]];j!=-1;j=edge[j].next)
{ //遍历i的相邻节点
v=edge[j].to;
if(dis[v]<dis[que[i]]+edge[j].w) //更新距离
dis[v]=dis[que[i]]+edge[j].w;
}
printf("%lld\n",dis[n+1]);
}
int main()
{
int i,j,u,v;
while(~scanf("%d%d",&n,&m))
{ //点数和边数
init();
for(i=1;i<=n;i++) scanf("%d",&w[i]); //输入点权
for(i=0;i<m;i++)
{
scanf("%d%d",&u,&v);
add(u,v,w[v]);
chu[u]++;
ru[v]++;
}
for(i=1;i<=n;i++)
{
if(ru[i]==0)
{ //在0点和入度为0的点之间加边
add(0,i,w[i]);
ru[i]++;
}
if(chu[i]==0)
{ //在出度为0的点和点n+1之间加边
add(i,n+1,0);
ru[n+1]++;
}
}
tuopu();
solve();
}
return 0;
}