优化————工程技术、经济管理、科学研究中的常见问题。(材料强度最大、运输费用最低、利润最高、风险最小)
用数学建模方法解决优化问题的过程
优化目标与决策 模型假设与建立 数学求解与分析
简单优化模型归结为函数极值问题,用微分法求解。
(书与数学规划的优化模型在第四章讨论)
讨论两个模型:不允许缺货模型和允许缺货模型。
不允许缺货的存贮模型:
问题:
已知某一部件的日需求量100件,生产准备费5000元,贮存费每日每件医院。若果生产能力远大于需求,而且不允许出现缺货,试安排该产品的生产计划,即每多少天生产一次(称为生产周期),每次产量多少,可使平均每天总费用最小。
要求:建立生产周期、产量与需求量、准备费、贮存费之间的关系。
分析:
- 一天一次,每天5000
- 10天一次,每天950
- 50天一次,每天2550
所以我们将目标函数设置为每天总费用的平均值。
模型假设:
- 产品每天的需求量为常数r;
- 每次准备费用为c1,每天每件产品贮存费为c2;
- T天为一周期(生产一次),每次Q件,当贮存量降为0时,Q件产品立即生产出来;
- 为方便起见,时间和产量都作为连续量处理。
建模目的:
r,c1,c2已知,求T,Q使得每天总费用的平均值最小。
模型建立:(离散问题连续化)
易得 Q=rT;
贮存量表示为:q(t)=-rx+rT;
一周期贮存费为:
一周期总费用:
每天总费用平均值(目标函数):
模型求解:
求最小值,此时,
(EOQ公式)
模型解释:
定性分析:c1增加,T,q增加,c2增加T,Q减少,r增加,T减少,Q增大
敏感性分析:讨论参数c1,c2,r有微笑变化时对生产周期T的影响。
用相对该表衡量结果对参数的敏感程度,T对c1的敏感度记作S(T,c1),定义为,
由易得到S(T,c1)=1/2.
作类似定义,可得到S(T,c2)=-1/2, S(T,r)=-1/2.
即c1增加百分之1,T增加百分之零点5.
可见,c1,c2,r的微小变化对生产周期T的影响是很小的。
模型应用:
r=100,c1=5000,c2=1,得到T=10,C=1000.
为什么不是前面的950呢?是因为我们将离散问题连续化了,并未考虑一天中何时储存。
允许缺货的贮存模型:
当贮存量降到零时仍有需求r,出现缺货,造成损失。
原模型假设:贮存量讲到0时,Q件立即生产出来
现假设:允许缺货,每天每件缺货损失费c3,缺货需补足
注意到模型中未出现生产成本,可以看作默认为在任何情况下,生产一件产品的生产成本相同。

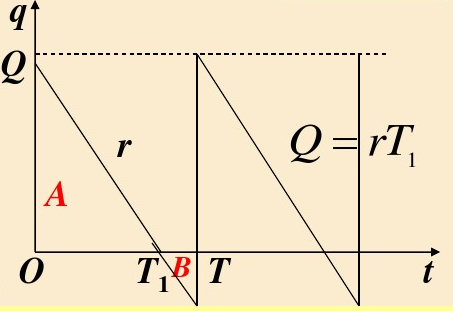
 (直接算面积也行)
(直接算面积也行)

