tarjan之有向图强连通缩点

一、强连通

在有向图G中，如果两个顶点间至少存在一条互相可达路径，称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。非强连通图有向图的极大强连通子图，称为强连通分量(strongly connected components)。

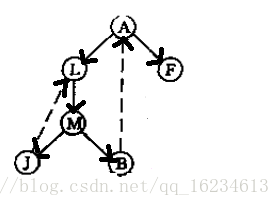
如上图，如果两个点成强联通，那么显然在树中就会存在一个环，图中L-M-J-L和A-L-M-B-A成环所以组成的强联通分量。

二、targan算法

由于强连通分量中的点相互连通，所以如果用dfs遍历到这个分量时，一定会回溯到已经遍历过的同属于这个分量的点

如图所示，图的一个强连通分量会在dfs时会形成以A为根节点的子树，我们只需要找出这个子树，并能够取出这个子树，也即利用Targan算法，Targan算法基于DFS和栈来实现，每次遍历到一个点时就把该点压栈。

首先建立两个数组DFN[] 和 LOW[], DFN[]用来记录点被遍历到的时候的时间，（会再定义一个全局变量做计时器），作用在于区分点，以及识别根，因为，当DFS走到强连通分量中的第一个点时，这个点的DFN[]一定是最小的，如图中的A。

LOW[]记录每个点能够回溯到的点的最小的DFN值，如B能够回溯到A，他的LOW实际就是A的DFN

LOW值一定小于DFN

scc[]表示某个点在缩点后的强连通分量坐标
sccnum表示缩点后强连通分量的个数
numinscc[]表示缩点后每个强连通分量中点的个数
一旦点的DFN不等于其LOW时，意味着他可以回溯到更早的点，所以这个点一定不是根节点。

当一个点的DFN==LOW时，这个点就是根，就将栈中该点及之上的所有点出栈，他们同属于一个强连通分量
(原文：https://blog.csdn.net/qq_36428237/article/details/80640401 )
代码

vector<int> G[10010];
stack<int> s;
int low[10010];
int dfn[10010];
int time = 0;
int scc[10010];
int sccnum = 0;
int visit[10010];
int numinscc[10010];
int outdegree[10010];
void Targan(int u)
{
    low[u] = dfn[u] = ++time;
    visit[u] = 1;
    s.push(u);
 
    for(int i=0;i<G[u].size();i++)
    {
        int v = G[u][i];
        if(visit[v] == 0)
        {
            Targan(v);
            low[u] = min(low[u],low[v]);
        }
        else if(visit[v] == 1&&scc[v] == 0)
            low[u] = min(low[u],dfn[v]);
    }
 
 
    int m;
    if(dfn[u] == low[u])
    {
        sccnum++;
        do
        {
            m = s.top();
            s.pop();
            scc[m] = sccnum;
            numinscc[sccnum]++;
        }while(m!=u);
    }
 
 
}
//需要计算出入度为0的点的话可以遍历每个点以及其儿子，判断是否于同一分量，再按照分量进行判断出入度
//另，一个图中需要添加max(in_0,out_0)条边以成为连通图