Dearboy is a game lover. Recently, he loves playing the game Lian Lian Kan. This game is played on a board with N*M grids, and lots of cards are put on the board in the grids. You should find a pair of the same cards, if not more than three segments can link this pair without passing any other cards, you can take this pair away from the board. (You may be puzzled about the meaning of not more than 3 segments, just refer to the figure below, in which we express some allowable links). Continue the process above, if you can clear all the cards, you win the game, otherwise you lose it.

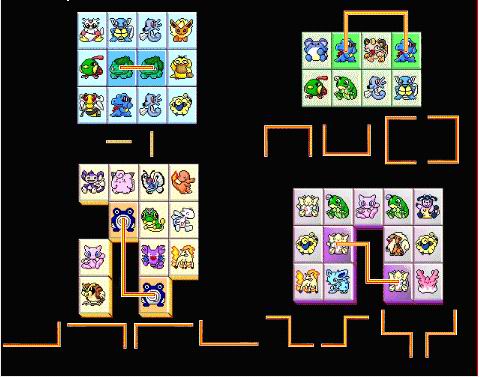
If you have played this game, you may know that sometimes the game has no solution and you are sure to lose. Dearboy is very boring about the games without solutions, so he asks you, a famous programmer, to tell him whether he can win the giving game phase or not.
Input
The input consists of multiple test cases. The first line of each test case contains two integers N and M (2 <= N, M <= 10), which denote the sizes of the game board. The next N lines give the board layout, with each line containing M characters. A character is one of the following: ‘*’ (an empty position), ‘A’, ‘B’, ‘C’, ’D’ (the cards, which imply that there are at most 4 different kinds of cards). Different letters represent different cards. The number of same cards may be odd, and there may be more than one pair of the same cards.
The input is terminated with two 0’s. This test case shoud not be processed.
Output
For each test case, print in one line “yes” if Dearboy can win the game, “no” otherwise.
Sample Input
6 8
********
*A**C***
**B*****
***B*D**
****D***
********
2 2
AB
BA
6 8
***A****
*A**C***
**B***C*
***B*D**
****D***
********
0 0
Sample Output
no
no
yes
题意:
- 连连看,但是转弯次数小于等于三次,而且外面一圈是封闭的。
题解:
- 先用dfs进行递归,枚举每个状态,在进入每个状态时,需要用bfs得到有几个能到达的点,并进行消除。
- 关键点在于回溯,也就是正确地理解回溯,在一个状态完成之后要将信息还原。
- 剪枝:图中有输入B的子块则立即回溯。
//#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include

