//#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<set>
#include<vector>
#include
<map>
#include<stack>
#include<queue>
#include<cmath>
#include<fstream>
#include<algorithm>
using namespace std;
#define rep(i,a,n) for(int i=a;i<=n;i++) #define per(i,a,n) for(int i=n;i>=a;i--)
#define CLR(a) memset(a,0,sizeof(a))
typedef long long ll;
typedef unsigned long long ull;
const int INF = 0x3f3f3f3f;
const int maxn=2010;
const int maxm=6000;
int tot=-1;//因为要利用成对的特性，所以只能从奇数开始，然后++tot作为第一条边
int head[maxn],ver[maxm],edge[maxm],Next[maxm];
int ans[1010][1010];
int v[maxn],incf[maxn],pre[maxn];
void addedge(int u,int v,int w) {
ver[++tot]=v,edge[tot]=w,Next[tot]=head[u],head[u]=tot;
ver[++tot]=u,edge[tot]=0,Next[tot]=head[v],head[v]=tot;
}
int maxflow=0;
int n,m;
int a[maxn];
int b[maxn];
int S,T;
bool bfs() {
memset(v,0,sizeof(v));
queue<int>q;
q.push(S);
v[S]=1;
incf[S]=INF;
while(q.size()) {
int x = q.front();
q.pop();
for(int i=head[x]; i!=-1; i=Next[i]) {
if(edge[i]) {
int y = ver[i];
if(v[y])continue;
incf[y]=min(incf[x],edge[i]);
pre[y]=i;
q.push(y),v[y]=1;
if(y==T)return 1;
}
}
}
return 0;
}
void update() {
int x=T;
while(x!=S) {
int i=pre[x];;
edge[i]-=incf[T];
edge[i^1]+=incf[T];
x = ver[i^1];
}
maxflow += incf[T];
}
int main() {
memset(head,-1,sizeof(head));
scanf("%d%d", &n,&m);
S=0,T=n*2+1;
int s1=0,s2=0;
rep(i,1,n) {
scanf("%d", &a[i]);
addedge(S,i,a[i]);
s1+=a[i];
}
rep(i,1,n) {
scanf("%d", &b[i]);
addedge(i,i+n,a[i]);//因为i节点前的流量只有a[i]，所以i到i与i到j的流量上限只有a[i]，所以上限只要大于a[i]即可
addedge(i+n,T,b[i]);
s2+=b[i];
}
if(s1!=s2) {
puts("NO");
return 0;
}
int u,v;
rep(i,1,m) {
scanf("%d%d", &u,&v);
addedge(u,v+n,a[u]);
addedge(v,u+n,a[v]);
}
while(bfs())update();
if(maxflow!=s1) {
puts("NO");
return 0;
}
printf("YES\n");
rep(i,1,n)
for(int j=head[i];j!=-1;j=Next[j])
if(ver[j]>n) ans[i][ver[j]-n]=a[i]-edge[j];
rep(i,1,n){
rep(j,1,n-1)
printf("%d ",ans[i][j]);
printf("%d\n",ans[i][n]);
}
return 0;
}
撰写
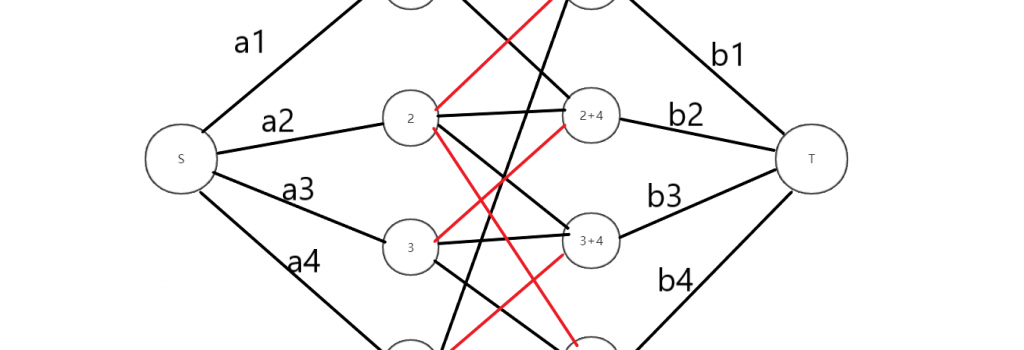
图中红色边为输入的反向边，而非反向弧,未标注的容量皆为>=ai
