2 seconds
256 megabytes
standard input
standard output
You came to the exhibition and one exhibit has drawn your attention. It consists of nn stacks of blocks, where the ii-th stack consists of aiaiblocks resting on the surface.
The height of the exhibit is equal to mm. Consequently, the number of blocks in each stack is less than or equal to mm.
There is a camera on the ceiling that sees the top view of the blocks and a camera on the right wall that sees the side view of the blocks.
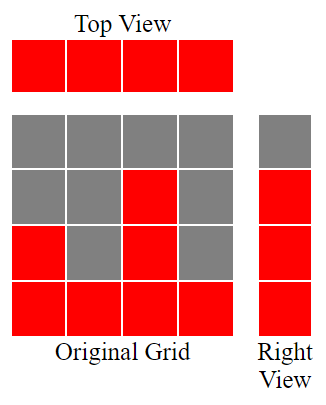
Note, that while originally all blocks are stacked on the floor, it is not required for them to stay connected to the floor after some blocks are removed. There is no gravity in the whole exhibition, so no block would fall down, even if the block underneath is removed. It is not allowed to move blocks by hand either.
The first line contains two integers nn and mm (1≤n≤1000001≤n≤100000, 1≤m≤1091≤m≤109) — the number of stacks and the height of the exhibit.
The second line contains nn integers a1,a2,…,ana1,a2,…,an (1≤ai≤m1≤ai≤m) — the number of blocks in each stack from left to right.
Print exactly one integer — the maximum number of blocks that can be removed.
5 6 3 3 3 3 3
10
3 5 1 2 4
3
5 5 2 3 1 4 4
9
1 1000 548
0
3 3 3 1 1
1
The following pictures illustrate the first example and its possible solution.
Blue cells indicate removed blocks. There are 1010 blue cells, so the answer is 1010.
Intention: Give you an integer n, m and a sequence of integers of length n. Each value in the sequence represents the number of squares per column. Ask to remove up to several squares so that the top view and the right view are unchanged. (Note that the block is not affected by gravity and can be left floating,but initially landed)
Answer:Sort first, from large to small, leaving only the topmost square for each column. If the topmost square is the same height as the previous one, mark it. If the height of the topmost square is smaller than the previous one, it is first filled with the mark, then the difference is calculated to determine the quantity to be saved in the previous column, and the last column is specially judged.
Code:
#include<algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cassert>
#include <cstdio>
#include <vector>
#include <string>
#include <cmath>
#include <queue>
#include <stack>
#include <set>
#include <map>
using namespace std;
#define P(a,b,c) make_pair(a,make_pair(b,c))
#define rep(i,a,n) for (int i=a;i<=n;i++)
#define per(i,a,n) for (int i=n;i>=a;i--)
#define CLR(vis) memset(vis,0,sizeof(vis))
#define MST(vis,pos) memset(vis,pos,sizeof(vis))
#define pb push_back
#define mp make_pair
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
typedef pair<int,pair<int,int> >pii;
typedef long long ll;
const ll mod = 1000000007;
const int INF = 0x3f3f3f3f;
ll gcd(ll a, ll b) { return b ? gcd(b, a%b) : a; }
const int maxn = 1e6+5;
int a[maxn];
int main(){
int n,h;
ll sum=0;
scanf("%d%d", &n,&h);
rep(i,1,n){
scanf("%d", &a[i]);
sum+=a[i];
}
ll cnt=0;
sort(a+1,a+n+1);
int q=0;
per(i,1,n-1){
int t=a[i+1]-a[i];
if(t==0){
q++;
cnt+=1;
}
else{
if(q>=t){
q-=t;
q++;
cnt+=1;
}else{
t-=q;
q=0;
cnt+=t;
}
}
}
if(a[1]>q)a[1]-=q;
else a[1]=1;
cout<<sum-cnt-a[1]<<endl;
return 0;
}
