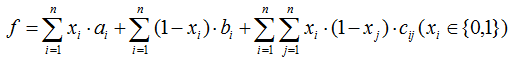MUTC 1 D – Matrix（最小割最大流 线性代数）

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include 
<map>
#include <set>
 
using namespace std;
 
const int maxn=2222;
const int maxm=2222222;
const int INF=1e9;
 
struct Edge{
    int from,to,cap,flow;
};
 
struct Dinic{
    int n,m,s,t;
    vector<Edge>edges;
    vector<int>G[maxn];
    bool vis[maxn];
    int d[maxn];
    int cur[maxn];
 
    void init(int n,int s,int t){
        this->n=n;
        this->s=s;
        this->t=t;
        for (int i=0;i<n;i++) G[i].clear();
        edges.clear();
        m=0;
    }
 
    void addedge(int from,int to,int cap){
        edges.push_back((Edge){from,to,cap,0});
        edges.push_back((Edge){to,from,0,0});
        m=edges.size();
        G[from].push_back(m-2);
        G[to].push_back(m-1);
    }
 
    bool BFS(){
        memset(vis,0,sizeof(vis));
        queue<int>que;
        que.push(s);
        d[s]=0;
        vis[s]=true;
        while (!que.empty()){
            int x=que.front();que.pop();
            for (int i=0;i<G[x].size();i++){ Edge& e=edges[G[x][i]]; if (!vis[e.to]&&e.cap>e.flow){
                    vis[e.to]=true;
                    d[e.to]=d[x]+1;
                    que.push(e.to);
                }
            }
        }
        return vis[t];
    }
 
    int DFS(int x,int a){
        if (x==t||a==0) return a;
        int flow=0,f;
        for (int& i=cur[x];i<G[x].size();i++){ Edge& e=edges[G[x][i]]; if (d[x]+1==d[e.to]&&(f=DFS(e.to,min(a,e.cap-e.flow)))>0){
                e.flow+=f;
                edges[G[x][i]^1].flow-=f;
                flow+=f;
                a-=f;
                if (a==0) break;
            }
        }
        return flow;
    }
 
    long long Maxflow(int s,int t){
        this->s=s;
        this->t=t;
        long long flow=0;
        while (BFS()){
            memset(cur,0,sizeof(cur));
            flow+=DFS(s,INF);
        }
        return flow;
    }
 
}solver;
 
int b[maxn][maxn];
int c[maxn];
 
int main()
{
    int T,n,s,t,a,x;
    long long sum;
    scanf("%d",&T);
    while (T--)
    {
        scanf("%d",&n);
        s=0;
        t=n+1;
        solver.init(n+2,s,t);
        sum=0;
        for (int i=1;i<=n;i++)
        {
            a=0;
            for (int j=1;j<=n;j++)
            {
                scanf("%d",&x);
                a+=x;
                solver.addedge(i,j,x);
            }
            sum+=a;
            solver.addedge(s,i,a);
        }
        for (int i=1;i<=n;i++)
        {
            scanf("%d",&x);
            solver.addedge(i,t,x);
        }
        printf("%I64d\n",sum-solver.Maxflow(s,t));
    }
    return 0;
}